
Los ordenadores fueron creados básicamente para expandir nuestros cerebros y aumentar nuestras habilidades cognitivas, originalmente fueron construidos para resolver problemas aritméticos, sin embargo, resultaron ser de gran utilidad para un sinfín de campos. A lo largo de los años, las computadoras se han hecho cada vez más poderosas y pequeñas a una escala increíble; basta con mencionar que hay más poder de procesamiento en un celular de hoy de lo que hubo en el mundo entero en la década de los ‘60 o que el alunizaje del Apollo 11 pudo haber sido llevado a cabo en un par de Nintendos (Walliman, 2017).
La informática es una ciencia que estudia lo que las computadoras pueden hacer, es un campo diverso y variado, no obstante, en este artículo nos enfocaremos en dos casos prácticos usando el machine learning, una rama de la Inteligencia Artificial (I.A.) que apunta a desarrollar algoritmos y técnicas para permitir a las computadoras aprender de grandes cantidades de datos y así, usar lo que han aprendido para hacer algo útil como relacionarlos, predecirlos o clasificarlos. Los programas con estas habilidades son extremadamente útiles en responder preguntas como: ¿Este mail es un spam? o ¿Qué video YouTube recomendará después de haber visto uno?; las sugerencias de la web no son coincidencias (Philbin, 2017).
El machine learning se subdivide en varias áreas donde distintos tipos de problemas pueden ser resueltos (Hederra, 2018), no obstante, para propósitos de este artículo, solo nos enfocaremos en el área del aprendizaje supervisado donde expondremos dos ejemplos prácticos, uno de regresión y otro de clasificación.
Uno de los aspectos más relevantes de la estadística es el análisis de la relación o dependencia de variables. Es por esto, que resulta de interés conocer el efecto que una o más variables pueden causar sobre otra, e incluso predecir en mayor o menor grado valores de una variable a partir de otra. Para este propósito, una de las técnicas más utilizadas es el ajuste de polinomios o regresión lineal, sin embargo, este método, como muchos otros, al basarse solo en un modelamiento de una función matemática, no suelen representar de la mejor manera la incertidumbre de los datos, se basan en relaciones que son sensibles a valores atípicos, no manejan de buena manera la aleatoriedad, conllevan a un sobreajuste del modelo y, por consiguiente, demuestran un exceso de error.

Es por lo anterior, que parece más razonable representar la aleatoriedad o incertidumbre de los datos a través de una herramienta matemática que se especializa en ella: las probabilidades. La importancia de enfocar la regresión a través de la perspectiva de las probabilidades, es que tiene el poder de reducir considerablemente los problemas de la regresión clásica en términos de minimización del error de un pronóstico dado.
Antes de entrar a definir como se comporta una regresión dentro del aprendizaje supervisado, es importante definir algunos conceptos. Llamaremos set de entrenamiento (training set) a un conjunto de datos de un largo de N puntos {x1,…,xn } el cual es utilizado para ajustar los parámetros (o pesos) de un modelo adaptativo. Por otra parte, expresaremos la categoría de un punto usando un vector objetivo t, el cual representa la imagen de un punto dado definiendo que solo existe un valor objetivo t para cada valor de x. La forma de la función f(x) es determinada durante la fase de entrenamiento (training o learning phase) basado en los datos de entrenamiento (traning data). Una vez que el modelo es entrenado se puede determinar la identidad de las nuevas imágenes, las cuales se les conoce comúnmente como el set de prueba (test set).
Una técnica de regresión notable para poder predecir una variable a partir de otras, es la regresión bayesiana que, explicándola de una forma simplista, se basa en evaluar la incertidumbre de los parámetros del modelo (o los pesos) w después de haber observado los datos D en la forma de una probabilidad posterior p(w│D). En otras palabras, esta técnica posee una inclusión de un conocimiento previo de los datos observados dando así una probabilidad a los parámetros del modelo. Los alcances matemáticos detrás de este tipo de regresiones son bastante profundos, por lo que se escapan del marco del presente artículo, no obstante, Bishop (2006) ofrece una completa justificación detrás de este tipo de regresiones.
Predecir la resistencia hidrodinámica residual en la etapa inicial del diseño de un buque, posee un gran valor para poder evaluar el rendimiento de éste y estimar la potencia propulsora requerida. Para este caso disponemos de los siguientes datos de entrada (o de entrenamiento): la posición longitudinal del centro de flotabilidad, el coeficiente prismático, la relación eslora-desplazamiento, la relación calado-manga, la relación eslora-manga y número de Froude, todos adimensionales.
Como los datos de entrada son limitados, validar el entrenamiento de los datos no fue factible a través de un set de validación, por lo que se utilizó la validación cruzada para tomar aleatoriamente parte de los datos que fueron ocupados para validar el modelo (la otra parte fue ocupada para el entrenamiento). La técnica de la validación cruzada consiste en tomar los datos disponibles y dividirlos en S grupos e iterar en todas las opciones posibles, promediando así las puntuaciones de desempeño de los S intentos. La predicción de la resistencia hidrodinámica se muestra en la Figura 1.
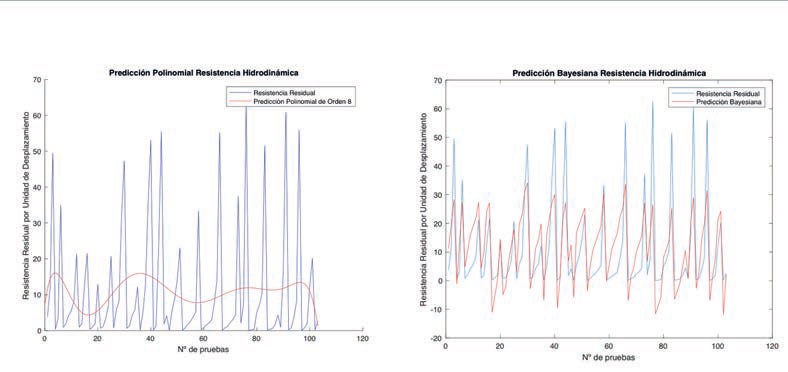
Figura 1: Regresión polinominal versus regresión bayesiana
Podemos apreciar la notable diferencia que existe en tratar de modelar la resistencia hidrodinámica residual a través de un polinomio (izquierda) y como se comporta el modelo de predicción a través de la regresión bayesiana (derecha); el error de pronóstico del primero es evidente. No obstante, parte del rendimiento de una predicción se mide en base al error del modelo con respecto a los datos originales; una de las medidas mas utilizadas es el Root Mean Square Error (RMSE) que mide la discordancia entre la función f(x,w), dado cualquier valor w, y los datos del set de entrenamiento. Los rendimientos de ambos son reflejados en la Tabla 1.
| Tipo de Regresión | RMSE |
| Regresión Lineal (Polinomio Orden 8) | 17,3% |
| Regresión Bayesiana | 8,67% |
| Tabla 1: RMSE regresión lineal y bayesiana. | |
A pesar de no existir una gran diferencia en los errores, el problema de la modelación polinomial de forma f(x,w)=wo+w1 x+w2 x2+…⋯+wM xM subyace en que a medida que subimos el orden del polinomio sus parámetros w comienzan a crecer desmedidamente, provocando así un sobre ajuste del modelo, en otras palabras, la función f(x) se adaptará de mejor forma a los datos de entrada y habrá sin duda menos error, sin embargo, no representará la realidad de la tendencia de los datos originales (de hecho, en este caso, claramente no la representa). Además, cualquier nuevo dato de entrada cambiará dramáticamente los valores de los parámetros w, y por consiguiente todo el modelo.
Por otra parte, lo verdaderamente interesante de la predicción bayesiana es que los parámetros w son adaptativos y se calculan a través de los datos de entrada (características físicas) entrenándolos con una parte de los datos de nuestra variable objetivo (resistencia hidrodinámica residual). Con estos parámetros definidos, la predicción bayesiana, explicada bajo un enfoque simplista, se conforma solo a través de la multiplicación de los datos de prueba con los parámetros w de nuestro modelo adaptativo. El comportamiento del modelo entrenado bayesiano es claramente mas cercano a la tendencia original de los datos de entrada.
El objetivo de la clasificación es tomar un vector de entrada x y asignarlo a una clase discreta K de las Ck clases donde k=1,…,K. En el escenario más común, se considera que la entrada es asignada a una sola clase, por lo tanto, el espacio de clasificación se divide en regiones de decisión Rk cuyos límites se denominan límites o superficies de decisión (decision boundaries).
La clasificación lineal consiste básicamente en que las superficies de decisión son funciones lineales del vector de entrada x y, por lo tanto, están definidas por hiperplanos dimensionales (D-1) dentro de un espacio de entrada de dimensión D. En el problema de regresión visto anteriormente, la variable objetivo t era simplemente un vector de números reales que deseábamos predecir, sin embargo, en el caso de la clasificación, existen varias formas de utilizar las variables objetivo para representar las etiquetas de cada clase. Para el caso de los problemas de dos clases, el más conveniente es la representación binaria en la que existe una única variable objetivo t∈{0,1} donde t=1 representa la clase C1 y t=0 representa la clase C2.
Para abordar el problema de clasificación lineal y asignar cada vector x a una clase específica, la forma más simple de lograrlo es a través de una función discriminante (discriminant function) la que en este caso será lineal. En términos simples, un discriminante no es mas que una función que toma un vector de entrada x y lo asigna a una de las clases K, denotada como Ck.
Por otra parte, el Support Vector Machine (SVM), que pertenece a la familia de los clasificadores lineales, es una técnica que se hizo bastante popular hace varios años atrás por resolver problemas tanto de clasificación como regresión. Su propiedad mas importante es que puede determinar los parámetros de un modelo a través de una optimización convexa, es decir, cualquier solución local también será un óptimo global. En grandes rasgos, la idea general de este tipo de clasificadores es que utiliza funciones matemáticas Kernel que permiten convertir un problema de clasificación no lineal en el espacio dimensional original, en un sencillo problema de clasificación lineal en un espacio dimensional mayor, en otras palabras, el SVM busca un hiperplano óptimo que pueda separar las clases.
Las extensiones matemáticas relacionadas a las representaciones de un discriminante lineal y un SVM y, como estos logran clasificar son bastante profundas e implican conceptos que salen del marco del presente artículo, no obstante, Bishop (2006), al igual que el caso de la predicción, ofrece también una completa demostración de este proceso.
Los procesos que implican el reconocimiento de contactos en un sonar, se mantiene como una tarea altamente demandante debido a un entorno de naturaleza confusa, cambiante, con un sinfín de variables y llena de incertidumbre. En este artículo, se desarrolló un clasificador lineal de dos clases (discriminante lineal) y un SVM para clasificar si los patrones captados desde un sonar activo, de frecuencia modulada, bajo diferentes ángulos y condiciones de ruido, pertenecen a una mina o a una roca. Estos datos poseen la particularidad de haber sido captados bajo diferentes ángulos y cada punto (dato) representa la energía dentro de una banda de frecuencia particular integrada sobre un cierto período de tiempo.
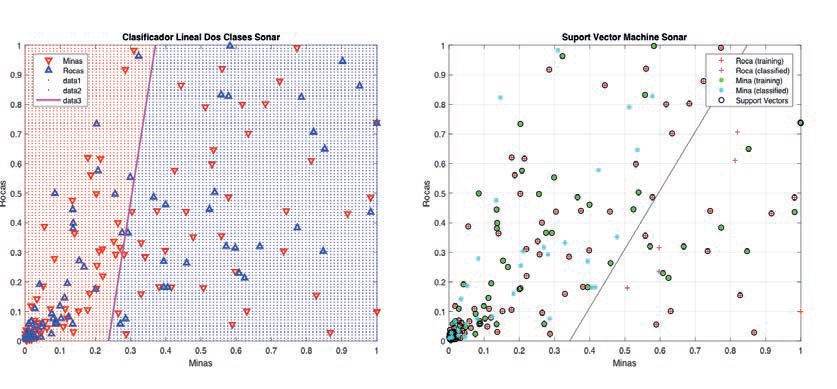
Figura 2: Clasificador linea de dos clases y un SVM.
Se puede apreciar como ambos clasificadores discriminan las dos clases de interés arrojando clasificaciones aparentemente parecidas, no obstante, parte del rendimiento de un clasificador se basa en analizar sus probabilidades de arrojar un error de clasificación, es decir, el error cuando un vector de entrada que pertenece a C1 se le asigna a la clase C2 o viceversa. El resultado de ambos clasificadores se muestra en la tabla 2.
| Clasificador Lineal de Dos Clases | Verdadero Mina | Verdadero Roca |
| Clasificado Mina | 0,51 | 0,49 |
| Clasificado Roca | 0,47 | 0,53 |
| Clasificador Support Vector Machine | Verdadero Mina | Verdadero Roca |
| Clasificado Mina | 0,57 | 0,43 |
| Clasificado Roca | 0,41 | 0,59 |
| Tabla 2: Matriz de error clasificador lineal de dos clases y SVM. | ||
Queda en evidencia que ambos clasificadores se comportan de manera similar, sin embargo, el clasificador SVM al basarse en métodos Kernel, tiende a obtener mejores resultados que un clasificador con discriminante lineal. Como es de notar, el error de clasificación es muy significativo, casi un 45%, lo que deja entrever dos elementos a considerar: el primero, que prueba el escaso entrenamiento que tuvieron los clasificadores con los datos disponibles y el segundo, que habla sobre lo dificultoso que resulta la clasificación de señales en un sonar.
En el presente articulo, se revisaron dos ejemplos prácticos para evidenciar el potencial del aprendizaje supervisado, no obstante, ambos no son más que muestras elementales de todas las técnicas y áreas existentes en el campo del machine learning. El caso de clasificación desarrollado en este artículo trataba solo de una discriminación entre dos clases, no obstante, la situación real dista mucho de esto. Para poder configurar un clasificador que pueda discriminar entre un sinfín de clases y variables de entorno, se necesita algo mucho más que un clasificador lineal. Se habla mucho del Deep Learning, el cual tiene la capacidad de lograr entrenarse con una gran cantidad de variables, no obstante, estas técnicas funcionan bajo los mismos principios aquí expuestos.
Hace 30 años, los ordenadores no poseían el potencial suficiente para que los procesos involucrados en el aprendizaje fueran realmente efectivos. Sin embargo, actualmente tenemos procesadores con una capacidad increíble, la inteligencia artificial es un campo que debe ser explorado especialmente en el ámbito militar (Pugh, 1987). A juicio del autor, es trascendental desarrollar en el corto plazo algoritmos propios, capaces de pronosticar sucesos o resultados a través de nuestros registros históricos y clasificadores que sean capaces de reconocer patrones en las señales acústicas, electrónicas y telecomunicaciones (Arancibia, 2005); este avance lograría incrementar significativamente las capacidades de nuestros sistemas de información, procesos de mantenimiento, sensores, entre muchas otras.
Para desarrollar los algoritmos de regresión y clasificación, se utilizó el programa MatLab R2017b en el cual se ocuparon algunas funciones predefinidas por el programa. Los datos ocupados para el entrenamiento de ambos ejemplos, fueron extraídos desde fuentes abiertas. En el caso de la predicción, se ocuparon 103 experimentos que fueron realizados en el Delft Ship Hydromechanics Laboratory en los Países Bajos. En el caso de la clasificación se utilizaron 180 señales de minas y rocas, respectivamente, provenientes de distintos patrones; estos datos provienen del Salk Institute, University of California en colaboración de la Allied-Signal Aerospace Technology Center. Para entrenar los datos en el caso de la predicción, se utilizó la validación cruzada (K-Folds) con 10 iteraciones, en el caso del SVM el entrenamiento fue realizado a base de una función predefinida antes de ejecutar la clasificación.
En el presente artículo, quedó en evidencia las potencialidades del uso del machine learning al ejemplificarlo a través de dos casos prácticos de aprendizaje supervisado. Con el constante avance de las capacidades computacionales será posible desarrollar algoritmos cada vez más complejos, los que podrán procesar de una mejor forma una mayor cantidad de datos y variables, permitiendo optimizar cada vez más este campo de la inteligencia artificial. Desarrollar nuestros propios algoritmos y ocupar estas tecnologías pareciera ser algo que debería ocuparnos en un corto plazo. Habiendo visto muy de cerca las capacidades de algunas de nuestras universidades, bastaría un buen grupo de trabajo integrado y un tiempo de dedicación razonable para lograrlo; esto está totalmente a nuestro alcance. Finalmente, cabe destacar que todas estas técnicas no sustituyen, bajo ninguna medida, el buen juicio de una persona en la toma de decisiones; solo constituye una ayuda y una herramienta importante para este proceso.
La estadística actual indica que los niveles de narcotráfico vía marítima han aumentado en Chile en los últimos años (Mi...
“El crimen organizado se combate como región o no se combate (Tohá, 2024)1" Miles de millones de personas utilizan...
¿Qué entendemos por “inteligencia”? Básicamente es la capacidad de abstraer, discernir, discriminar, aprender, crear, an...
“La inteligencia artificial es el futuro no solo para Rusia, sino para toda la humanidad. Trae consigo enormes oportunid...
NOTA del Autor: Este articulo ha sido completamente escrito por una aplicación de Inteligencia Artificial (chatGPT). Se ...
Versión PDF
Año CXXXX, Volumen 143, Número 1009
Noviembre - Diciembre 2025
Inicie sesión con su cuenta de suscriptor para comentar.-